Bubble formation in stagnant liquids

The formation and subsequent breakup of a bubble inside a stagnant liquid is the most studied con guration to produce bubbles, due to its simplicity and importance in many chemical engineering applications. For the particular case of small gas flow-rates, the bubble formation can be described by a two-stage phenomenon: an expansion is followed by a collapse stage (see the movie below). Just after the detachment of the previous bubble, the gas stem that remains attached to the injector tip grows during the expansion stage. This phase continuesuntil the bubble is large enough so that the upwards buoyancy force overtakes the downwards surface tension force. At this moment, a neck appears in the vicinity of the nozzle on the bubble surface and the dynamic collapse stage starts, in which the neck accelerates radially inwards until it collapses, producing the release of the main bubble. This break-up phenomenon is commonly known as pinch-off .

The last instants previous to the bubble "pinch-off" has been shown to present unexpected features and can not be described by a universal solution because it depends on the control parameters and also on the initial conditions in each particular case. 

We have examined the axisymmetric collapse in a quiescent water pool under constant gas flow rate conditions using the experimental facility sketched in figure 1:

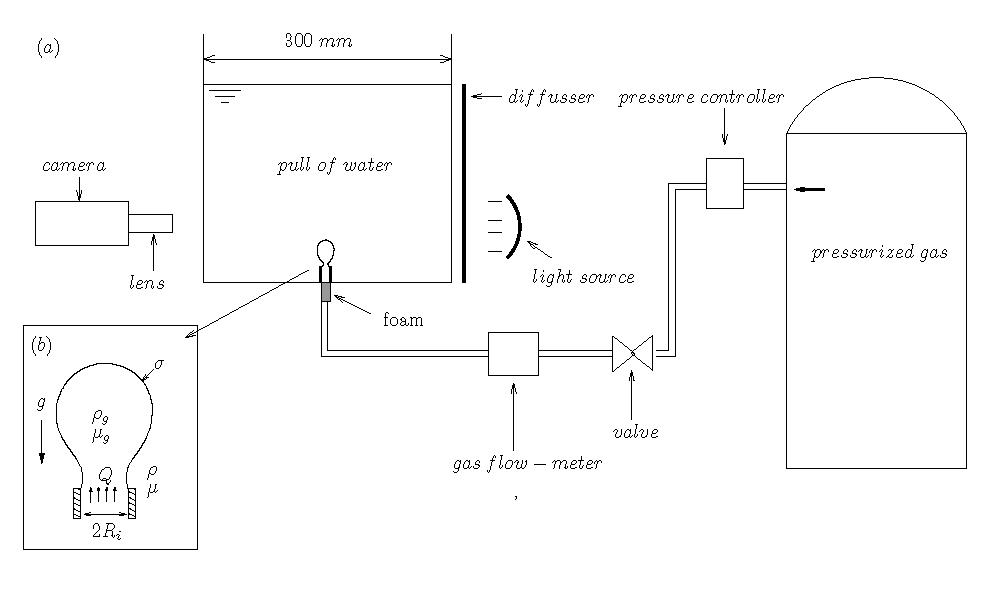
Figure 1. a) Sketch of the experimental set-up, and b) detail of a forming bubble, together with the definitions of the control parameters of the problem.

 

The experiments were recorded unsing a high-speed camera and two kinds of movies were recorded: 

Figure 2. Experimental visualizations of the collapse stage of an air bubble generated quasi-statically corresponding to the control parameters, Bond and Weber numbers, Bo=\rho gR_i^2/\sigma=0.012,We_Q = \rho\,Q^2/(\pi^2\,R_i^3\sigma)=0.005, respectively. a) Sequence of the global bubble shape and b) detail of the necking process

 

The dynamics of the last instants previous to pinch-off have been described using a theoretical model by J.M. Gordillo (Physics of Fluids 20, 112103 (2008)). For high Reynolds numbers Re\to\infty and without taking into account the gas inertia effects, the model consists of thes couple of 2 dimensional Raileigh-like equations:

\ln(R_0r_1)\frac{d\,\ln(R_0\dot{R}_0)}{ds}-1+\frac{2R_0(1-2R_0r_1)}{(R_0\dot{R}_0)^2}=0,\\\ln(R_0r_1)\frac{d\,\ln(R_0r_1)}{ds}-1+\frac{R_0}{(R_0\dot{R}_0)^2}=0

 where R_0 and r_1 are the minimum neck radius and half the axial curvature respectively, s=-\ln(R_0), \dot{R_0}=dR_0/dt is the radial velocity, Re_g=\rho_g\,V\,R_i/\mu_g, V=R_i/t^*_\sigma and Re=\rho\,V\,R_i/\mu. Length and time are made dimensionless with the nozzle inner radius,  R_i, and with the capillary time t_{\sigma}^*=(\rho R^3_i/\sigma)^{1/2} respectively.

This model has been shown to reproduce the experimental dynamics of the last instants as can be noticed in the next figure, where the neck radius, half the axial curvature and the radial velocity are ploted as a function of the time remaining to pinch-off.

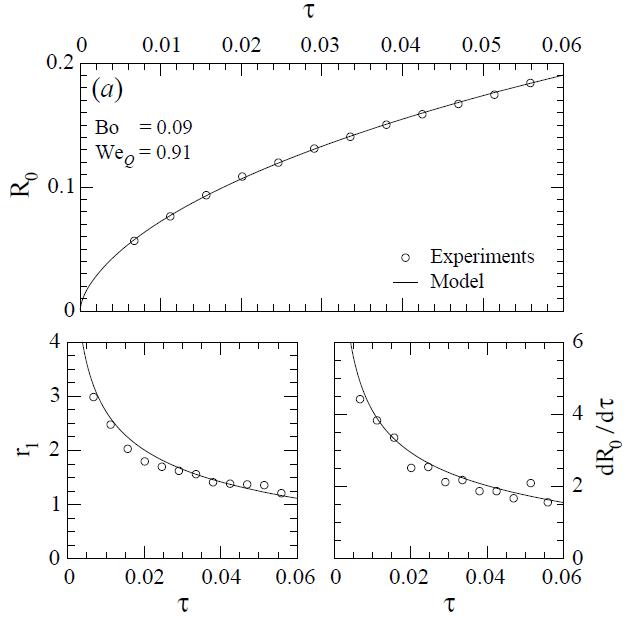
Figure 3. Comparison of the time evolution of R_0, r_1 and \dot{R}_0 obtained experimentally (symbols) with those given by the model (solid lines)

Moreover, we have investigated the effect of the liquid viscosity on the bubble pinch-off, which results to slow down the process and has tipically been characterized by an increase of the effective exponent \alpha of the power law R_0\propto\tau^{\alpha}. 

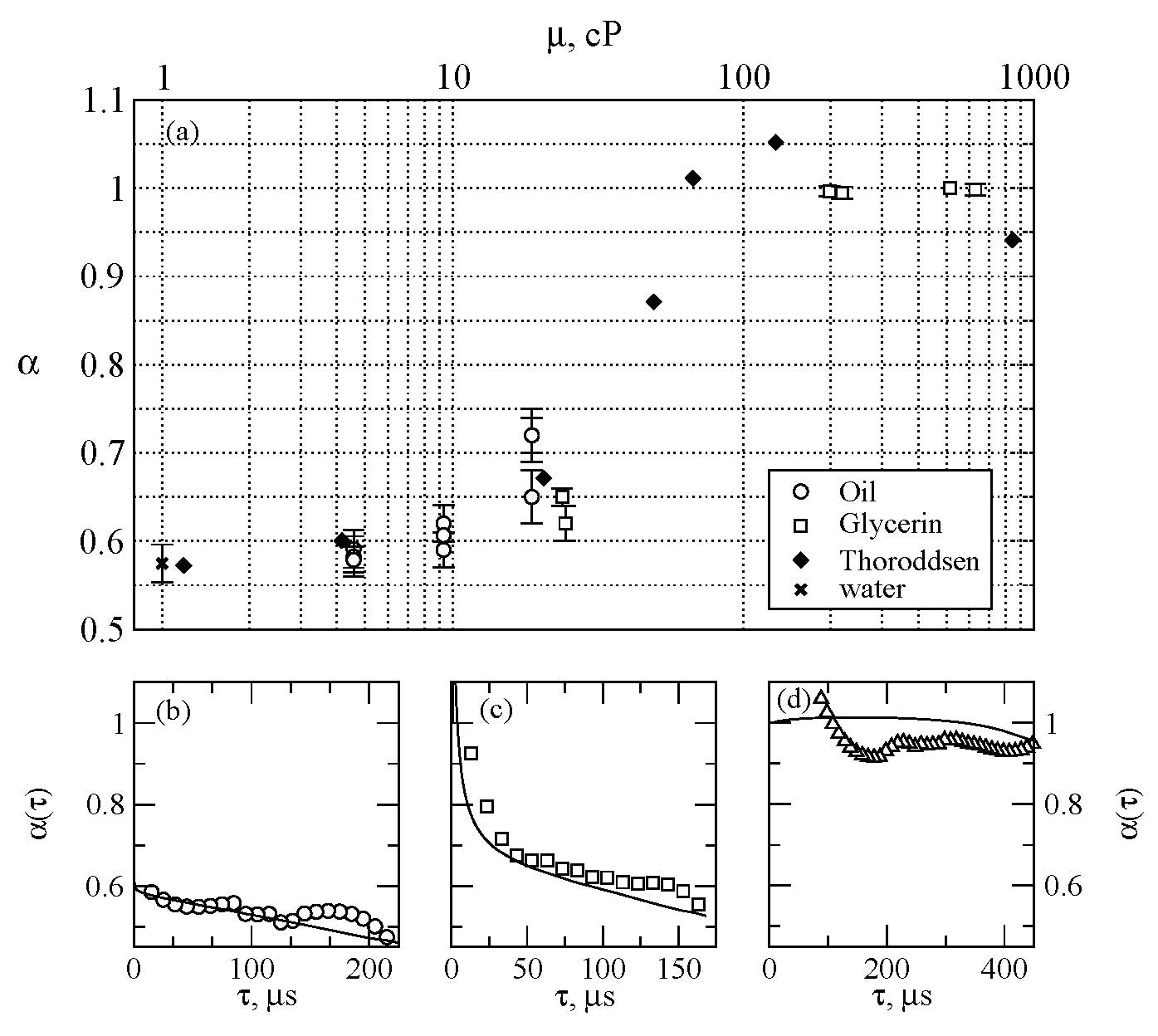
Figure 4. (a) Effective exponent of the power law as a function of liquid viscosity for all the experiments performed with silicone oil (open circles) and some of the experiments performed with water/glycerin mixtures (open squares). The cross shows an experiment performed with water and solid diamonds correspond to data taken from Thoroddsen et. al. Time evolution of the instantaneous exponent, \alpha(\tau) corresponding to (b) water, (c) and (d) two water-glicerine mixtures. Solid lines indicate the results of the integration of the theoretical model.

Nevertheless, the effective exponent is found to strongly depend on the control parameters and on the initial conditions.  Moreover, the local exponent, \alpha(\tau) = d\ln R_0/d\ln \tau, varies significantly during the collapse of the neck mainly in the case of liquids with viscosities in the range 10-100 cP. Consequently, a power law with a constant effective exponent is not a good choice to describe the transition from inviscid to viscous bubble pinch-off.

 Therefore, we use a slight modification of the model proposed by Gordillo (2008)  to properly account for viscous effects:

\ln\left(R_0\,r_1\right)\frac{d\,\ln(R_0\,\dot{R}_0)}{d\,s}-1+\frac{2\,R_0\,\left(1-2R_0 r_1\right)}{\left(R_0\,\dot{R}_0\right)^2}+\frac{4\,Oh}{R_0\,\dot{R}_0}=0\,,

\left(\ln\left(R_0\,r_1\right)+\frac{2\,Oh}{R_0\,\dot{R}_0}\right)\frac{d\,\ln(R_0\,r_1)}{d\,s}-1+\frac{R_0}{\left(R_0\,\dot{R}_0\right)^2}+\frac{4\,Oh}{R_0\,\dot{R}_0}=0\,,

 where Oh=\mu/\sqrt{\rho\,\sigma\,R_i} is the Ohnesorge number. The model is able to reproduce the dynamics of the experiments for any value of the liquid viscosity:

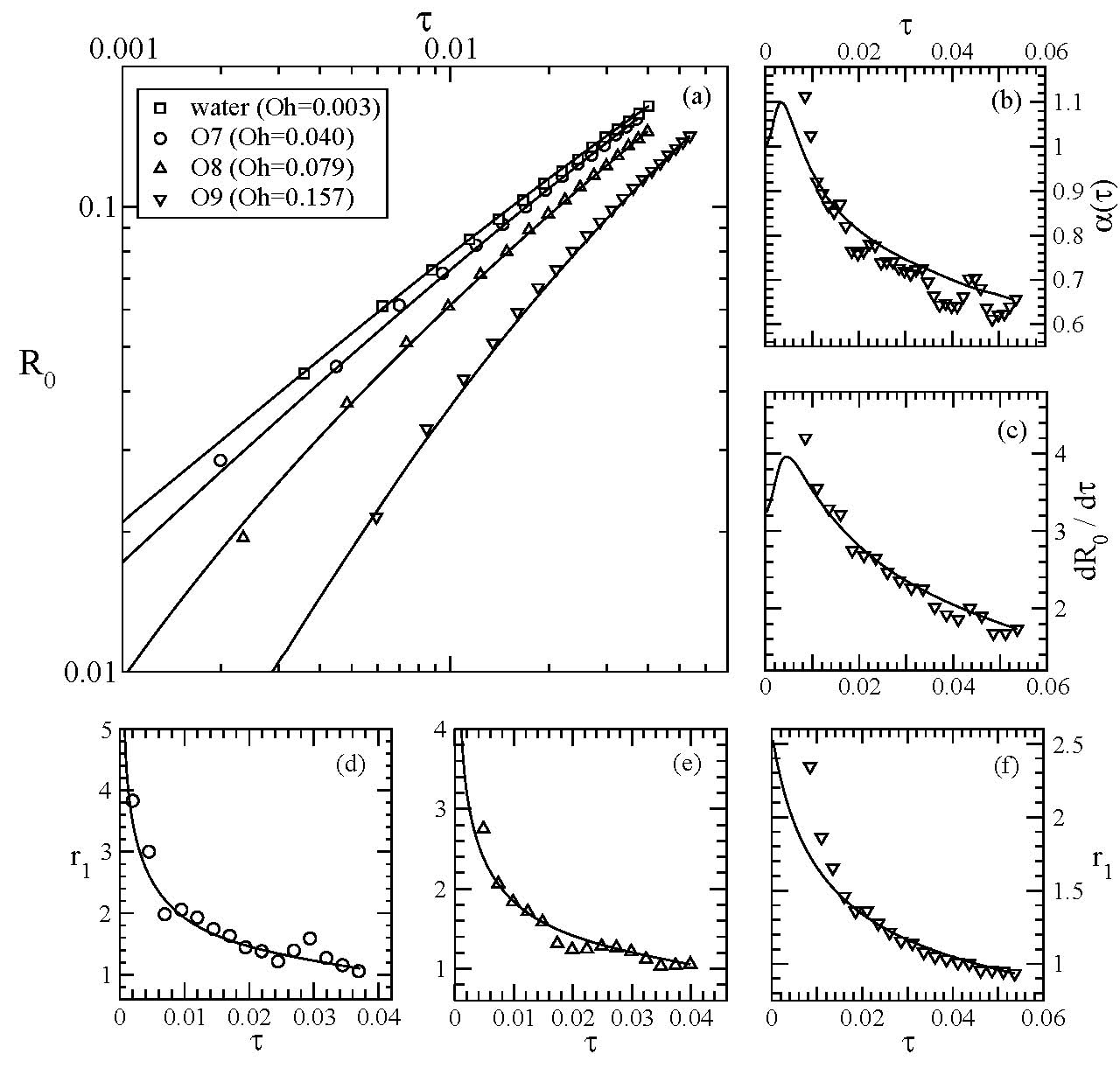
Figure 5. (a) Time evolution of the neck radius obtained experimentally (symbols), compared with the integration of the model (solid lines). Time evolution of (b) the local exponent, and (c) the radial velocity, corresponding to experiment O9. (d),(e),(f) Time evolution of r_1 for experiments O7, O8 and O9, respectively.

However, in most of the cases, the gas supply is neither at constant flow rate nor at constant pessure supply and, consequently, an exhaustive study of bubble formation under coupled conditions by means of experiments, theory and numerical simulations.

Researchers

Carlos Martínez Bazán
Alejandro Sevilla Santiago 
Rocío Bolaños Jiménez
José Carlos Cano Lozano
José Manuel Gordillo Arias de Saavedra (Universidad de Sevilla)

Supporting Projects

Spanish Ministry of Science and Innovation and European Funds. 

DPI2011-28356-C03-03, DPI2008-06624-C03-02, DPI2005-08654-C04-01.

Publications

  • R. Bolaños-Jiménez, A. Sevilla, J.M. Gordillo and C. Martínez-Bazán. Axisymmetric Bubble collapse in a Quiescent Liquid Pool. Part II. Experimental Study. Physics of Fluids 20, 11210 (2008). 
  • R. Bolaños-Jiménez, A.Sevilla, C. Martínez-Bazán, D. Van der Meer and J.M. Gordillo. The effect of liquid viscosity on bubble pinch-off. Physics of Fluids 21, 072103 (2009).